Cinemática directa e inversa de brazos robot
Autor: José OlinPublicado: 2022-11-28

Cuando trabajamos con brazos robot tenemos básicamente dos problemas a resolver.
Si conocemos el ángulo de cada una de las articulaciones y queremos calcular la posición de la pinza o efector final usamos Cinemática directa.
Si sabemos a donde queremos llevar el efector final y necesitamos calcular el ángulo que debe tener cada articulación, usamos Cinemática Inversa.
Al resolverlos nos llevamos la agradable sorpresa de que aquellas clases de trigonometría tienen aplicación en lo salvaje.
Para entender el concepto general del análisis cinemático usaremos el ejemplo de un brazo con 2 grados de libertad (g.d.l.) que se mueve en un plano.
Cinemática directa de un brazo de 2 g.d.l.
Consideremos un manipulador planar con dos articulaciones como el de la imagen.
Los ángulos de las articulaciones están denotados como \(\bf{q} := (\theta_1, \theta_2)\).
La posición y orientación del efector final (la pinza azul) están denotados como \(\bf{p} := (x,y,\theta)\)
El problema que resuelve la cinemática directa o FK es calcular la posición y orientación p de la pinza, conociendo el ángulo de sus articulaciones q.
$$ FK: q \rightarrow p$$
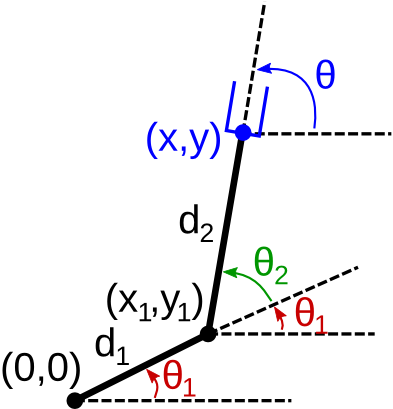
Aplicando trigonometría para el primer eslabón, tenemos que
$$ x_1 = d_1 cos(\theta_1) $$ $$ y_1 = d_1 sin(\theta_1) $$
De forma similar, para el segundo eslabón, tenemos:
$$ \begin{array}{rclcl} x & = & x_1 + d_2 \cos(\theta_1+\theta_2) & = & d_1 \cos(\theta_1) + d_2 \cos(\theta_1+\theta_2) \\ y & = & y_1 + d_2 \sin(\theta_1+\theta_2) & = & d_1\sin(\theta_1) + d_2 \sin(\theta_1+\theta_2) \\ \end{array} $$
Ahora programemos esto en Python con Spyder o tu editor favorito, para probarlo.
Función en Python para Cinemática directa
Creamos un archivo FuncionesCinematica.py en el que definiremos la función cinematicaDirecta() que recibe por parámetro los ángulos en grados del primer eslabón respecto al eje \(x\) y del segundo eslabón respecto al primero, es decir \(\theta_1 \) y \(\theta_2\) en la figura.
Consideraremos que el eslabón 1 es de 35 cm y el segundo de 30 cm.
El script hará las siguientes tareas:
- Convertir los ángulos de grados a radianes.
- Calcular la posición del extremo del primer eslabón \( (x_1, y_1) \).
- Calcular la posición del extremo del segundo eslabón (nuestro punto de interés) \( (x_2, y_2) \) .
- Devolver la posición del segundo eslabón y su ángulo respecto al eje x \( (x, y, \theta) \).
# FuncionesCinematica.py
def cinematicaDirecta(th1_deg, th2_deg):
"""
Params:
th1_deg: Angulo del primer eslabon en grados.
th2_deg: Angulo del segundo eslabon en grados.
"""
#Definición del largo de eslabones.
d1 = 0.35;
d2 = 0.30;
## 1. Convertir los ángulos de grados a radianes
th1 = math.radians(th1_deg);
th2 = math.radians(th2_deg);
## 2. Cálculo de la posición del eslabón 1
x1 = d1 * math.cos(th1)
y1 = d1 * math.sin(th1)
## 3. Cálculo de la posición del eslabón 2
x2 = x1 + d2 * math.cos(th1 + th2)
y2 = y1 + d2 * math.sin(th1 + th2)
## 4. Devolver la posicion y orientacion del efector final
return [x2, y2, math.degrees(th1 + th2)]
Ahora creemos un segundo script para probar la función, con algunos casos sencillos de verificar.
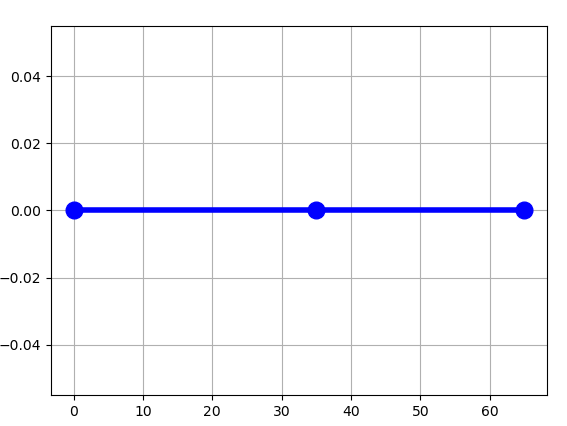
Caso 1
Ambos eslabones están paralelos al eje x.
$$ \theta_1 = 0, \theta_2=0 $$
# MainCinematica.py
from FuncionesCinematica import cinematicaDirecta
from math import radians
## Caso 1.
th1_deg = 0; # El primer eslabon esta horizontal al eje x
th2_deg = 0; # El segundo eslabon esta perpendicular al eslabon 1.
print(cinematicaDirecta(th1_deg, th2_deg))
Al ejecutar el script en Spyder o terminal nos devuelve:
[0.6499999999999999, 0.0, 0.0]
Esto es, el efecto final estaría a casi 65 cm en el eje x, es decir la suma del largo de los dos eslabones.
Nota: Debido al error por redondeo devuelve un valor muy cercanos pero no igual a 0.65. Podemos hacer que Spyder haga un redondeo a dos decimales y muestre 0.65, pero nos pareció una excelente oportunidad para recordar que las computadoras tienen sus límites.
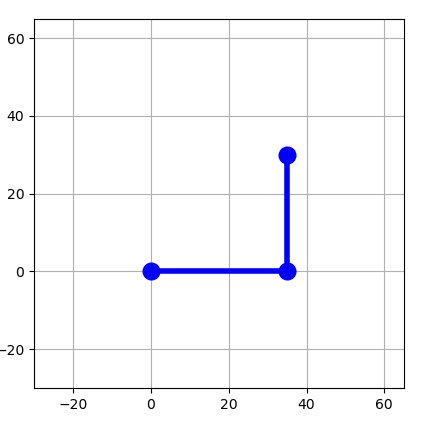
Caso 2
El primer eslabón está horizontal al eje x y el segundo perpendicular al eslabón 1.
$$ \theta_1 = 0, \theta_2=90 $$
th1_deg = 0; # El primer eslabon esta horizontal al eje x
th2_deg = 90 # El segundo eslabon esta perpendicular al eslabon 1.
print(cinematicaDirecta(th1_deg, th2_deg))
Al ejecutar el script debería devolvernos:
[0.35, 0.3, 90.0]
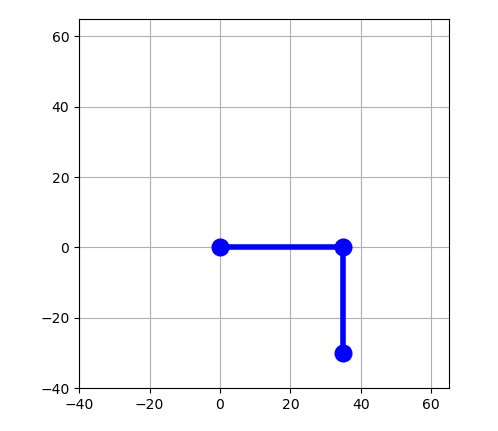
Caso 3
El primer eslabón esta horizontal al eje x y el segundo perpendicular al eslabón 1 pero en el sentido opuesto.
$$ \theta_1 = 0, \theta_2=-90 $$
th1_deg = 0; # El primer eslabon esta horizontal al eje x
th2_deg = -90; # El segundo eslabon esta perpendicular al eslabon 1.
print(cinematicaDirecta_ee(th1_deg, th2_deg))
Que nos devuelve:
[0.35, -0.3, -90.0]
Caso 4
El primer eslabón está a 45° y el segundo es paralelo al primero.
A 45° el seno y el coseno tienen el mismo valor, por lo que esperaríamos valores iguales para \(x_2\) y \(y_2\)
th1_deg = 45; # El primer eslabon está a 45°
th2_deg = 0; # El segundo eslabón está en la misma dirección respecto al primero.
print(cinematicaDirecta_ee(th1_deg, th2_deg))
En efecto, nos devuelve:
[0.4596194077712559, 0.4596194077712558, 45.0]
Todos los casos devuelven valores lógicos. Podemos pasar a la cinemática inversa.
Cinemática inversa de un brazo de 2 g.d.l
Si queremos colocar el extremo del segundo eslabón en alguna posición deseada \( \bf{p_{des}}:=(x_{des},y_{des}) \), (de momento, sin importar la orientación), encontrar los ángulos adecuados que debe tener cada articulación es el problema de la cinemática inversa.
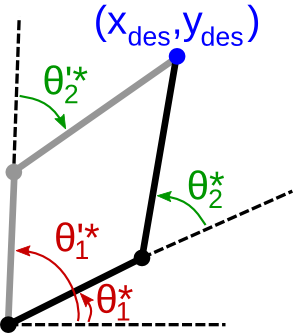
Recordando de la cinemática directa que
$$ \begin{array}{rclcl} x & = & x_1 + d_2 \cos(\theta_1+\theta_2) & = & d_1\cos(\theta_1) + d_2 \cos(\theta_1+\theta_2) \\ y & = & y_1 + d_2 \sin(\theta_1+\theta_2) & = & d_1\sin(\theta_1) + d_2 \sin(\theta_1+\theta_2) \\ \end{array} $$
A partir de aquí hay dos formas (que hemos usado) de encontrar la expresión para la cinemática inversa: la primera utiliza una identidad de suma y diferencia de ángulos y la segunda utiliza el teorema del coseno. La primera es más directa pero la segunda es más intuitiva gráficamente, así que veremos esta primero.
Cálculo de la cin. inversa usando ley de cosenos
Encontrando \(\theta_2\)
Consideremos en nuestro brazo ejempo se forma un triángulo entre los 2 eslabones y la recta del efector final al origen. Podemos utilizar el teorema del coseno, que es una generalización del teorema de Pitágoras, para encontrar el ángulo \(\theta_2\).
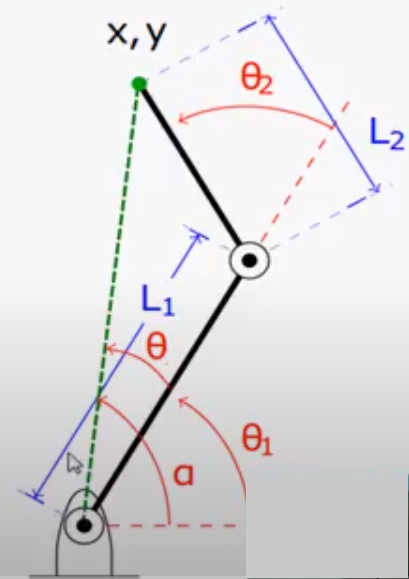
Sea \(c\) el largo de la recta que une el efector final con el origen, por un lado tenemos que por teorema de pitágoras:
$$ c^2 = x^2 + y^2 $$
Y por otro lado, dado el teorema del coseno
Dado un triángulo ABC cualquiera, siendo \(\alpha, \beta, \gamma\), los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:
$$ c^2 = a^2 + b^2 - 2ab cos(\gamma) $$
En el modelo del brazo, y reemplazando \(c^2\) por \(x^2 + y^2\) la equivalencia sería:
$$ x^2 + y^2 = L_1^2 + L_2^2 - 2 L_1 L_2 cos(180-\theta_2) $$
Dado que por reflexión:
$$ cos(180-\theta_2) = -cos(\theta_2) $$
Tendríamos: $$ x^2 + y^2 = L_1^2 + L_2^2 + 2 L_1 L_2 cos(\theta_2) $$
Y encontramos una expresión para \(\theta_2\)
$$ \theta_2 = arccos \left( \frac{x^2 + y^2 - L_1^2 - L_2^2}{2 L_1 L_2} \right) $$
Encontrando \(\theta_1\)
Para encontrar \(\theta_1\) consideremos que:
$$ \theta_1 = \alpha - \theta \tag{eq. 1} $$
$$
\alpha = arctan \left( \frac{y}{x} \right)
\tag{eq. 2}
$$

Y usando teorema de los senos
$$ \frac{sin A}{a} = \frac{sin B}{b} = \frac{sin C}{c} $$
Podemos definir que:
$$ \frac{sin \theta}{L_2} = \frac{sin(180-\theta_2)}{\sqrt{x^2 + y^2}} $$
$$ \frac{sin \theta}{L_2} = \frac{sin(180-\theta_2)}{\sqrt{x^2 + y^2}} = \frac{sin\theta_2}{\sqrt{x^2 + y^2}} $$
De donde
$$ \theta = arcsin \left(\frac{L_2 sin\theta_2}{\sqrt{x^2 + y^2}} \right) \tag{eq. 3} $$
Cuyo valor ya podemos calcular, pues en este punto ya conoceríamos \(\theta_2\).
Y podríamos resolver la ec. 1, pues el valor de \(\alpha \) se calcularía con la posición deseada (x, y), y hemos encontrado la expresión para calcular \(\theta\).
$$ \theta_1 = arctan \left( \frac{y}{x} \right) - arcsin \left( \frac{L_2 sin\theta_2}{\sqrt{x^2 + y^2}} \right) $$
Ecuaciones para \( \theta_1 \) y \(\theta_2 \)
$$ \theta_2 = arccos \left( \frac{x^2 + y^2 - L_1^2 - L_2^2}{2 L_1 L_2} \right) $$
$$ \theta_1 = arctan \left( \frac{y}{x} \right) - arcsin \left( \frac{L_2 sin\theta_2}{\sqrt{x^2 + y^2}} \right) $$
Calculamos primero \(\theta_2\), pues \(\theta_1\) depende de ella.
Cálculo de la cin. inversa usando identidad de suma y diferencia
La segunda forma de definir las ecuaciones para la cinemática inversa es usar la identidad de suma y diferencia, también conocida como teorema de adición y sustracción, que establece:
Que puede aplicarse a las ecuaciones de la cinemática directa:
$$ \begin{array}{rcl} x_{des} & = & d_1 \cos(\theta_1^{*}) + d_2 \cos(\theta_1^{*}+\theta_2^{*}) \\ y_{des} & = & d_1\sin(\theta_1^{*}) + d_2 \sin(\theta_1^{*}+\theta_2^{*}) \end{array} $$
Encontrando \(\theta_2 \)
Elevando ambos lados de las ecuaciones al cuadrado tenemos:
$$ \begin{array}{rcl} x_{des}^2 + y_{des}^2 &=& d_1^2 + d_2^2 + 2d_1d_2\left(\cos(\theta_1^*)\cos(\theta_1^*+\theta_2^*) + \sin(\theta_1^*)\sin(\theta_1^*+\theta_2^*)\right) \end{array} $$
Y usando el cuarto caso de la identidad de suma y diferencia, considerando \( \alpha = \theta_1^* + \theta_2^* \) y \(\beta = \theta_1^* \)
$$ \begin{array}{rclcl} x_{des}^2 + y_{des}^2 &=& d_1^2 + d_2^2 + 2d_1d_2\left(\cos(\theta_1^*)\cos(\theta_1^*+\theta_2^*) + \sin(\theta_1^*)\sin(\theta_1^*+\theta_2^*)\right) \ &=& d_1^2 + d_2^2 + 2d_1d_2 \cos(\theta_2^*) \end{array} $$
De donde podemos despejar el valor de \(\theta_2^*\) como:
$$ \cos(\theta_2^*) = \frac{x_{des}^2+y_{des}^2-d_1^2-d_2^2}{2 d_1 d_2} $$
Sin embargo, hay tres casos posibles:
Si \( \frac{x_{des}^2+y_{des}^2-d_1^2-d_2^2}{2 d_1 d_2} > 1 \), la cinemática inversa no tiene solución; lo que intuitivamente significaría que la posición deseada está fuera del alcance del brazo.
De otra forma, si es menor o igual a 1, hay dos soluciones para \( \theta_2^* \)
$$ \theta_2^* = \pm \arccos\left( \frac{x_\mathrm{des}^2+y_\mathrm{des}^2-d_1^2-d_2^2}{2d_1d_2} \right) $$
Encontrando \(\theta_1 \)
Calculando \(\theta_2\) y aplicando estos cálculos, encontramos la expresión de \( \theta_1\):
$$ \theta_1^* = \arctan2(y_{des},x_{des}) - \arctan2(k_2,k_1) $$
donde: $$ k_1 := d_1 + d_2\cos(\theta_2^*) \quad \mathrm{and} \quad k_2 := d_2\sin(\theta_2^*) $$
Ecuaciones para \( \theta_1 \) y \(\theta_2 \)
$$ \theta_2^* = \pm \arccos\left( \frac{x_\mathrm{des}^2+y_\mathrm{des}^2-d_1^2-d_2^2}{2d_1d_2} \right) $$
$$ \theta_1^* = \arctan2(y_{des},x_{des}) - \arctan2(k_2,k_1) $$
Que son equivalentes a las encontradas con el primer método, aunque la función arctan2 permite calcular los ángulos en todos los cuadrantes, mientras que la arctan sólo en uno de los cuadrantes del plano cartesiano.
Función en Python para Cinemática inversa
# FuncionesCinematica.py
def cinematicaInversa(x_des, y_des):
num = (x_des * x_des) + (y_des * y_des) - (d1 * d1) - (d2 * d2)
den = 2 * d1 * d2
cociente = num / den
th1_inv = 0
th2_inv = 0
if cociente <= 1.0:
th2_inv = math.acos(cociente)
k1 = d1 + d2 * math.cos(th2_inv)
k2 = d2 * math.sin(th2_inv)
th1_inv = math.atan2(y_des, x_des) - math.atan2(k2, k1)
print("x_des: " + format(x_des, '.4f') +
", y_des: " + format(y_des, '.4f') +
", th1: " + format(th1_inv, '.4f') +
", th2: " + format(th2_inv, '.4f') )
else: # Si cociente > 1, no hay soluciones.
print("No alcanzable")
th1_inv = 0;
th2_inv = 0;
return np.array([th1_inv, th2_inv])
Invocamos la función en los 4 casos probados con la cinemática directa, para los cuales conocemos las soluciones y vemos si la función encuentra los valores correctos.
Caso 1
$$p_{des} = [0.65, 0.0] $$
Una nota interesante en este caso es que si intentamos calcularla con 0.65, el cociente es ligeramente mayor a 1 (por centésimas de milésima), pero suficiente para que el programa lo considere fuera de rango. Así que usaremos un valor ligeramente menor, como el que devolvió la cin. directa.
np.set_printoptions(precision = 5, suppress=True) # Para redondear la salida de print.
x_des = 0.6499999999;
y_des = 0.0;
th_rad = cinematicaInversa(x_des, y_des)
th_deg = np.degrees(th_rad)
print(cinematicaInversa(x_des, y_des))
Notar que la función de cinemática inversa devuelve valores en radianes, así que los convertimos a grados antes de imprimirlos en pantalla.
Resultado
[-0., 0.]
Caso 2
$$ p_{des} = [0.35, 0.3] $$
x_des = 0.35;
y_des = 0.30;
th_rad = cinematicaInversa(x_des, y_des)
th_deg = np.degrees(th_rad)
print(th_deg)
Resultado:
[-0. 90.]
Caso 3
$$ p_{des} = [0.35, -0.3] $$
x_des = 0.35;
y_des = -0.3;
th_rad = cinematicaInversa(x_des, y_des)
th_deg = np.degrees(th_rad)
print(th_deg)
Resultado:
[-81.20259 90. ]
Esta solución no corresponde con los valores de la cinemática directa, sin embargo, como puede verse en la figura, es otra solución válida de acuerdo a las dimensiones de los eslabones.
En la práctica debemos elegir entre las soluciones matemáticas posibles, cuáles son mecánicamente válidas para el brazo.
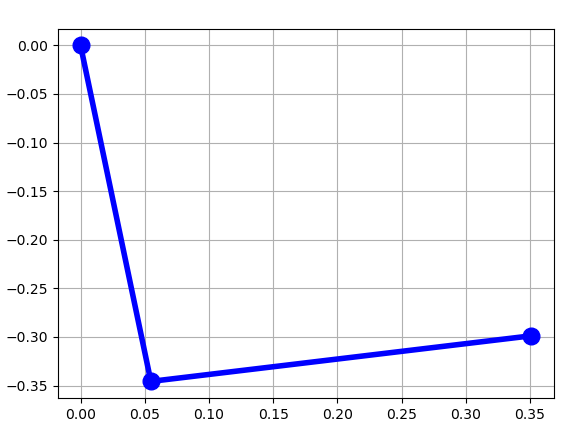
Caso 4
$$ p_{des} = [0.45961, 0.45961] $$
x_des = 0.45961;
y_des = 0.45961;
th_rad = cinematicaInversa(x_des, y_des)
th_deg = np.degrees(th_rad)
print(th_deg)
Resultado:
[44.6606 0.73536]
Recapitulando la cinemática inversa
Como puede verse, las ecuaciones de la cinemática inversa son bastante más complejas de encontrar que las de la directa.
Además, mientras que una configuración de articulaciones q tiene una posición única resultante, una posición deseada \(p_{des}\) puede corresponder con ninguna, una o múltiples configuraciones de las articulaciones.
Conclusiones
La idea de este post es que tengamos una idea general de cómo se calcula la cinemática de un robot manipulador, echando un vistazo general con un ejemplo de 2 g.d.l., a la forma de obtener estas ecuaciones y cómo implementarlas en Python.
En un próximo post veremos cómo definir la cinemática para robots más complejos usando la librería Robotics Toolbox en Python.
Referencias
OS Robotics. Forward kinematics





